Rumus suku ke n barisan tingkat 2 - Belajar Matematika Online

Untuk menentukan rumus suku ke n barisan tingkat 2 tentu kalian sudah mengenal terlebih dahulu tentang barisan aritmatika dan materi persamaan linier tiga variabel dengan menggunakan metode subtitusi atau eliminasi. Karena materi-materi tersebut merupakan prasyarat untuk mempelajari barisan tingkat 2.

Apa yang di maksud barisan Bertingkat?

Barisan bilangan adalah deretan bilangan-bilangan yang membentuk pola tertentu seperti contoh di bawah ini:

Pada barisan diatas memiliki beda = 2 atau kita mengenalnya dengan barisan aritmatika atau barisan aritmatika tingkat 1, tentu saja rumus suku ke-n barisan ini bisa di tentukan dengan rumus suku ke-n barisan aritmatika.

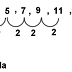
Perhatikan bentuk barisan berikut : 1 , 2 , 4 , 7 , 11 , ...

Pada barisan di atas beda barisan pada tingkat pertama tidak sama sehingga perlu di tentukan kembali beda nya hingga tinggkat barulah di peroleh beda yang tetap yaitu 1 , barisan bilangan seperti inilah yang di sebut barisan tingkat 2 atau barisan aritmatika tingkat 2. Lalu bagaimana menentukan rumus suku ke-n atau U_n barisan tingkat 2?

Untuk menentukan suku ke-n dari barisan tingkat 2 di gunakan rumus berikut:

Rumus di atas adalah cara cepat menghitung barisan aritmatika tingkat 2 , yang contoh soalnya akan di bahas di bawah ini.

Contoh soal barisan aritmatika tingkat 2

Agar lebih jelas simak pembahasan soal di bawah ini

Contoh 1

Tentukan suku ke-n dari barisan 2 , 3, 6 , 11 , 18 , 27 , ...

[Penyelesaian]

Diketahui U₁= a = 2 ; U₂ = 3 dan U₃ = 6

Dari penyelesaian di atas di peroleh 3 persamaan yaitu:

Selanjutnya dengan cara eliminasi persamaan (2) - (1):

Selanjutnya dengan cara eliminasi persamaan (3) - (2):

Selanjutnya dengan cara eliminasi persamaan (5) - (4):

Selanjutnya subtitusikan a = 1 ke persamaan (4) di peroleh :

Jadi rumus suku ke-n barisan bilangan 2 , 3, 6 , 11 , 18 , 27 , ...

adalah U_n = n² – 2n + 3

Dengan mengetahui rumus suku ke-n barisan tingkat 2 dapat di tentukan suku-suku lainnya dengan mudah misalnya :

Menetukan rumus cepat barisan tingkat 2

Untuk menentukan rumus cepat barisan tingkat 2 sebaiknya perhatikan terlebih dahuli pembahasan di bawah:

Dari rumus U_n= an² + bn + c kita tentukan empat suku pertama yaitu:

U₁ = a.(1)² + b.1 + c = a + b + c

U₂ = a.(2)² + b.2 + c = 4a + 2b + c

U₃ = a.(3)² + b.3 + c = 9a + 3b + c

U₄ = a.(4)² + b.4 + c = 16a + 4b + c

Setelah di tentukan empat suku pertama maka:

U_{1 ,}U₂, U₃, U₄, …

Dari uraian di atas dapat di tentukan rumus cepat untk mencari suku ke-n barisan tingkat 2 yaitu:

a + b + c = U₁

3a + b = beda

2a = Konstanta

Sekarang rumus di atas akan di gunakan untuk menyelesaikan soal pada contoh 1

Tentukan suku ke-n dari barisan 2 , 3, 6 , 11 , 18 , 27 , ...

[Penyelesaian]

Tentukan terlebih dahulu beda barisan tingkat 2 di atas:

Dari uraian di atas di ketahui U₁ = 2 ; beda = 1 dan konstanta = 2 , maka:

a + b + c = 2 …… (1)

3a + b = 1 …… (2)

2a = 2 …… (3)

Dari persamaan (3) di peroleh a = 1

Subtitusikan a = 1 ke persamaan (2) di peroleh b = -2

Subtitusikan a = 1 dan b = -2 ke persamaan (1) di peroleh c = 3

Kemudian subtitusikan a = 1 ; b = -2 dan c = 3 ke rumus U_n

U_n = an² + bn + c

U_n = 1.n² + (-2)n + 3

U_n = n² -2n + 3

Cukup mudah ya mencari rumus suku ke n barisan tingkat 2 , semoga mudah di mengerti dan di pahami untuk menambah pengetahuan kalian tentang barisan bertingkat.

Terimakasih anda telah membaca artikel tentang Rumus suku ke n barisan tingkat 2. Jika ingin menduplikasi artikel ini diharapkan anda untuk mencantumkan link https://soulmath4u.blogspot.com/2021/03/Cara%20cepat%20Menentukan%20Rumus%20suku%20ke%20n%20barisan%20tingkat%202%20.html?m=0. Terimakasih atas perhatiannya.