Integral Substitusi

Teknik Pengintegralan dengan Integral Subtitusi

Integral subtitusi merupakan salah satu teknik penyelesaian integral khusus termasuk juga teknik integral parsial. Oleh karena itu prasyarat mempelajari materi integral subtitusi ini yaitu integral tak tentu fungsi aljabar , integral tak tentu fungsi trigonometri serta integral tertentu wajib anda kuasai terlebih dahulu. Jika lupa silahkan di review lagi ya!

Integral Subtitusi  Aljabar

Integral subtitusi  aljabar adalah pengintegralan yang dapat dirubah ke dalam bentuk ∫ f(u) du. Dibawah ini adalah teorema integral subtitusi ,

Langkah-langkah pengintegralan dengan teknik integral subtitusi

Secara umum teknik integral subtitusi menggunakan dua langkah dibawah ini:

1.Menentukan fungsi u = g(x) sehingga ∫ f(g(x)) g’(x) dx dapat dirubah menjadi  ∫ f(u) du.

2.Selesaikan bentuk  ∫ f(u) du

Agar lebih jelas perhatikan contoh soal integral subtitusi dibawah ini!

Soal-soal dan Pembahasan integral subtitusi

Tentukan integral-integral berikut dengan teknik integral subtitusi!

1.

[Penyelesaian]

Subtitusikan (1) dan (2) ke soal semula,

2.

[penyelesaian]

Subtitusikan (1) dan (2) ke soal semula,

3.

[Penyelesaian]

Subtitusikan (1) dan (2) ke soal semula,

4.

[Penyelesaian]

Subtitusikan (1) dan (2) dan (3) ke soal semula,

5.

[Penyelesaian]

Soal no 5 ini menggunakan fungsi bilangan e . Subtitusikan (1) dan (2) ke soal semula,

6.

[Penyelesaian]

Soal no 6  ini menggunakan fungsi logaritma natural. Subtitusikan (1) dan (2) ke soal semula,

Perlu dicatat bahwa teknik integral subtitusi juga berlaku untuk integral tertentu baik fungsi aljabar maupun fungsi trigonometri untuk fungsi trigonometri rumus-rumus dasar trigonometri sangat diperlukan.

Integral substitusi Fungsi Trigonometri 

Hitunglah nilai setiap integral tertentu dibawah ini dengan teknik integral subtitusi!

1.

[Penyelesaian]

2.

[Penyelesaian]

Ubah dahulu soal diatas dengan manipulasi aljabar sebagai berikut:

Subtitusikan (2) dan (3) ke (1),

3.

[Penyelesaian]

Ubah dahulu soal diatas dengan manipulasi aljabar sebagai berikut:

Subtitusikan (2) dan (3) ke (1),

4.

[Penyelesaian]
Ubah dahulu soal diatas dengan manipulasi aljabar sebagai berikut:





Subtitusikan (2) dan (3) ke (1), 

5.

[Penyelesaian]
Buat terlebih dahulu permisalan integral subtitusi nya,



Subtitusikan (1) dan (2) ke soal awal:

Integral Substitusi Trigonometri  

Teknik pengintegralan berikutnya adalah integral subtitusi trigonometri yaitu integral yang memuat bentuk-bentuk seperti dibawah ini,

Hasil subtitusinya seperti tabel 1 dibawah ini:

Contoh soal dan Pembahasan Integral Substitusi Trigonometri   

Tentukanlah integral – integral dibawah ini!

1.

[Penyelesaian]

Subtitusikan (1) dan (2) ke soal awal,

2.

[Penyelesaian]





Subtitusikan (1) dan (2) ke soal awal,

3.

[Penyelesaian]



Subtitusikan (1), (2) dan (3) ke soal awal,

4.

[Penyelesaian]

5.

[Penyelesaian]

Demikian pembahasan integral subtitusi, jika ada kesalahan konsep atau pun dalam pembahasan silahkan berikan komentar di kolom komentar. Like juga ya fanspage facebook nya, dan semoga materi integral subtitusi ini bermanfaat.

⊡ Materi yang masih berkaitan:

∯ Integral parsial

Terimakasih anda telah membaca artikel tentang Integral Substitusi . Jika ingin menduplikasi artikel ini diharapkan anda untuk mencantumkan link https://soulmath4u.blogspot.com/2014/03/integral-substitusi.html?m=0. Terimakasih atas perhatiannya.

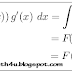Belajar Matematika Online
Published: 2014-03-02T17:31:00-08:00
Title:Integral Substitusi
Rating: 5 On 22 reviews

Artikel Terkait